Breve Biografía de James Clerk Maxwell y sus Ecuaciones
James Clerk Maxwell
James Clerk Maxwell (Edimburgo, Reino Unido; 13 de junio de 1831–Cambridge,Inglaterra; 5 de noviembre de 1879) fue un físico británico conocido principalmente por haber desarrollado la teoría electromagnética clásica, sintetizando todas las anteriores observaciones, experimentos y leyes sobre electricidad, magnetismo y aun sobre óptica, en una teoría consistente. Las ecuaciones de Maxwell demostraron que la electricidad, el magnetismo y hasta la luz, son manifestaciones del mismo fenómeno: el campo electromagnético. Desde ese momento, todas las otras leyes y ecuaciones clásicas de estas disciplinas se convirtieron en casos simplificados de las ecuaciones de Maxwell. Su trabajo sobre electromagnetismo ha sido llamado la "segunda gran unificación en física", después de la primera llevada a cabo por Isaac Newton. Además se le conoce por la estadística de Maxwell-Boltzmann en la teoría cinética de gases.
Maxwell fue una de las mentes matemáticas más preclaras de su tiempo, y muchos físicos lo consideran el científico del siglo XIX que más influencia tuvo sobre la física del siglo XX habiendo hecho contribuciones fundamentales en la comprensión de la naturaleza. Muchos consideran que sus contribuciones a la ciencia son de la misma magnitud que las de Isaac Newton y Albert Einstein. En 1931, con motivo de la conmemoración del centenario de su nacimiento, Albert Einstein describió el trabajo de Maxwell como «el más profundo y provechoso que la física ha experimentado desde los tiempos de Newton».
Ecuaciones de Maxwell
Ley de Gauss para Campo Eléctrico
La ley de Gauss explica la relación entre el flujo del campo eléctrico y una superficie cerrada. Se define como flujo eléctrico (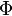 ) a la cantidad de fluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico (
) a la cantidad de fluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico ( ) que pasa por una superficie S. Matemáticamente se expresa como:
) que pasa por una superficie S. Matemáticamente se expresa como:
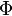 ) a la cantidad de fluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico (
) a la cantidad de fluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico ( ) que pasa por una superficie S. Matemáticamente se expresa como:
) que pasa por una superficie S. Matemáticamente se expresa como:
La ley dice que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga (q) o la suma de las cargas que hay en el interior de la superficie y la permitividad eléctrica en el vacío (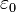 ), así:
), así:
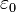 ), así:
), así:Ley de Gauss para el Campo Magnético
Experimentalmente se llegó al resultado de que los campos magnéticos, a diferencia de los eléctricos, no comienzan y terminan en cargas diferentes. Esta ley primordialmente indica que las líneas de los campos magnéticos deben ser cerradas. En otras palabras, se dice que sobre una superficie cerrada, sea cual sea ésta, no seremos capaces de encerrar una fuente o sumidero de campo, esto expresa la inexistencia del monopolo magnético. Al encerrar un dipolo en una superficie cerrada, no sale ni entra flujo magnético por lo tanto, el campo magnético no diverge, no sale de la superficie. Entonces la divergencia es cero. Matemáticamente esto se expresa así:
donde  es la densidad de flujo magnético, también llamada inducción magnética. Es claro que la divergencia sea cero porque no salen ni entran vectores de campo sino que este hace caminos cerrados. El campo no diverge, es decir la divergencia de B es nula.
es la densidad de flujo magnético, también llamada inducción magnética. Es claro que la divergencia sea cero porque no salen ni entran vectores de campo sino que este hace caminos cerrados. El campo no diverge, es decir la divergencia de B es nula.
 es la densidad de flujo magnético, también llamada inducción magnética. Es claro que la divergencia sea cero porque no salen ni entran vectores de campo sino que este hace caminos cerrados. El campo no diverge, es decir la divergencia de B es nula.
es la densidad de flujo magnético, también llamada inducción magnética. Es claro que la divergencia sea cero porque no salen ni entran vectores de campo sino que este hace caminos cerrados. El campo no diverge, es decir la divergencia de B es nula.
Su forma integral equivalente:
Como en la forma integral del campo eléctrico, esta ecuación sólo funciona si la integral está definida en una superficie cerrada.
Ley de Faraday-Lenz
La ley de Faraday nos habla sobre la inducción electromagnética, la que origina una fuerza electromotriz en un campo magnético. Es habitual llamarla ley de Faraday-Lenz en honor a Heinrich Lenz ya que el signo menos proviene de la Ley de Lenz. También se le llama como ley de Faraday-Henry, debido a que Joseph Henry descubrió esta inducción de manera separada a Faraday pero casi simultáneamente. Lo primero que se debe introducir es la fuerza electromotriz ( ), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:
), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:
 ), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:
), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así: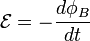 ,
,
como el campo magnético es dependiente de la posición tenemos que el flujo magnético es igual a:
 .
.
Además, el que exista fuerza electromotriz indica que existe un campo eléctrico que se representa como:
con lo que finalmente se obtiene la expresión de la ley de Faraday:
Lo que indica que un campo magnético que depende del tiempo implica la existencia de un campo eléctrico, del que su circulación por un camino arbitrario cerrado es igual a menos la derivada temporal del flujo magnético en cualquier superficie limitada por el camino cerrado.
El signo negativo explica que el sentido de la corriente inducida es tal que su flujo se opone a la causa que lo produce, compensando así la variación de flujo magnético.
Ley de Ampére-Maxwell
Ampére formuló una relación para un campo magnético inmóvil y una corriente eléctrica que no varía en el tiempo. La ley de Ampére nos dice que la circulación en un campo magnético ( ) a lo largo de una curva cerrada C es igual a la densidad de corriente (
) a lo largo de una curva cerrada C es igual a la densidad de corriente (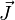 ) sobre la superficie encerrada en la curva C, matemáticamente así:
) sobre la superficie encerrada en la curva C, matemáticamente así:
 ) a lo largo de una curva cerrada C es igual a la densidad de corriente (
) a lo largo de una curva cerrada C es igual a la densidad de corriente (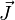 ) sobre la superficie encerrada en la curva C, matemáticamente así:
) sobre la superficie encerrada en la curva C, matemáticamente así:
donde 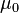 es la permeabilidad magnética en el vacío.
es la permeabilidad magnética en el vacío.
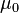 es la permeabilidad magnética en el vacío.
es la permeabilidad magnética en el vacío.
Pero cuando esta relación se la considera con campos que sí varían a través del tiempo llega a cálculos erróneos, como el de violar la conservación de la carga. Maxwell corrigió esta ecuación para lograr adaptarla a campos no estacionarios y posteriormente pudo ser comprobada experimentalmente por Heinrich Rudolf Hertz.
Maxwell reformuló esta ley así:
En el caso específico estacionario esta relación corresponde a la ley de Ampére, además confirma que un campo eléctrico que varía con el tiempo produce un campo magnético y además es consecuente con el principio de conservación de la carga.






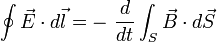

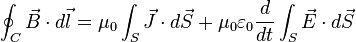




0 comentarios: